Concept Learning and General to Specific Ordering-Part(3)

General-to-Specific Ordering of Hypotheses

In the last post, we said that all concept learning problems share 1 thing in common regarding their structure, and it is the fact that we can order the hypotheses from the most specific one to the most general one. This will enable the machine learning algorithm to explore the hypothesis space exhaustively, without having to enumerate through each and every hypothesis in this space, which is absolutely impossible when you have an infinitely large hypothesis space. Now, we will talk about the general-to-specific ordering and show you how we can use this to define a sense of order among our hypotheses in a hypothesis space in any concept learning problem.

As a reminder, take a look at our old example regarding Joe wanting to play golf on a specific day or not. Remember that we would like to learn the concept of Play about Joe.

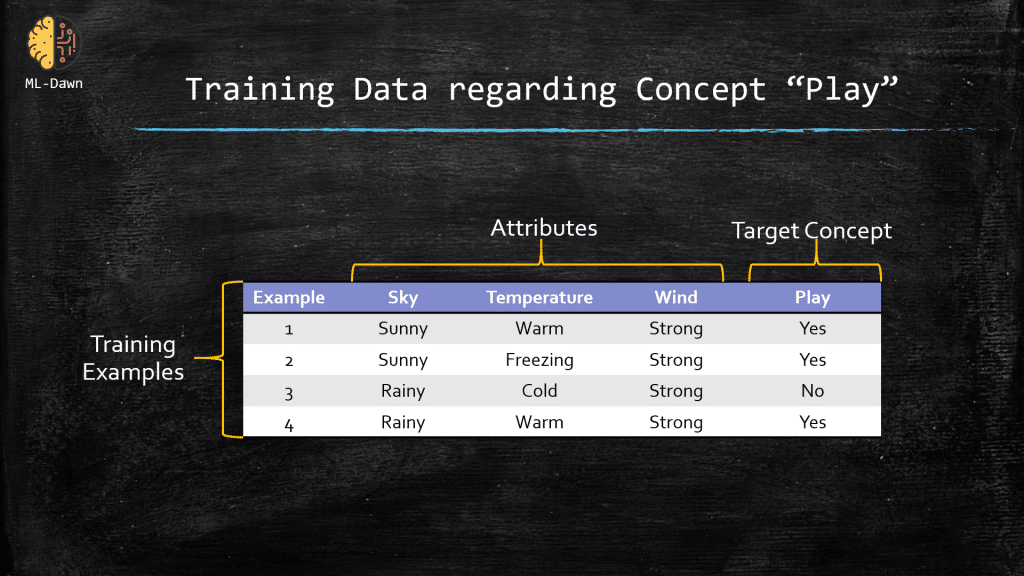
Now, consider the following 2 hypotheses:

h₁ = <Rainy, Warm, Strong>

h₂ = <Rainy, ?, Strong>

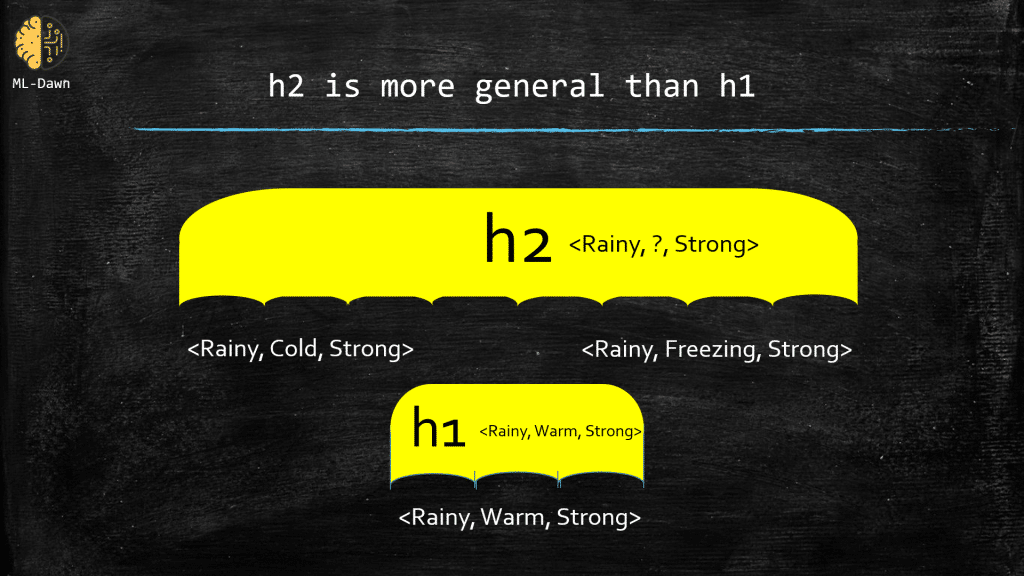
The question is which instances and how many of them are classified positive by each one of these hypotheses (i.e., satisfy these hypotheses). For h₁, only example number 4 is satisfactory, while for h₂, both example 3 and 4 are satisfactory and classified as positive. Why is that? What is the difference between these 2 hypotheses? The answer lies into the strictness of the constraints that are imposed by each one of these hypotheses. As you can see, h₁ imposes more constraints compared to h₂! Naturally, h₂ is able to classify more examples as positive than h₁! Actually, in this example, we can claim the following:

“If an example could satisfy h₁, it will FOR SURE satisfy h₂, but NOT the other way around”

This is because h₂ is more general than h₁. This has been demonstrated below: h₂ encompasses more possibilities than h₁. If we have an instance with the values: <Rainy, Freezing, Strong>, h₂ will classify it as positive but h₁ will not be satisfied by it. But when h₁ classifies an instance as positive , say, <Rainy, Warm, Strong>, then it is certain that h₂ will also classify it as positive.

More-General-than-or-Equal-to Relationship

Let’s remind ourselves of 2 crucial definitions:

For a given example x in the instance space X, and a hypothesis h in the hypothesis space H, we say that x satisfies h if and only if h(x) = 1.
We define the “more general than or equal to” relationship between 2 hypotheses, and we base it on the sets of examples that satisfy each one of the 2 hypotheses.

Now, here is the long-awaited definition:

Hypothesis h_j is more general than or equal to the hypothesis h_k, if and only if any instance x in the instance space X that can satisfy h_k (i.e., h_k(x) = 1) also satisfies h_j (i.e., h_j(x) = 1)

We can show this relationship with the following notation:

h_j ≥_g h_k

Where g is short for general. There are cases where a hypothesis is more general than the other one, but NOT equal to it. Below you can see the definitions for both cases:

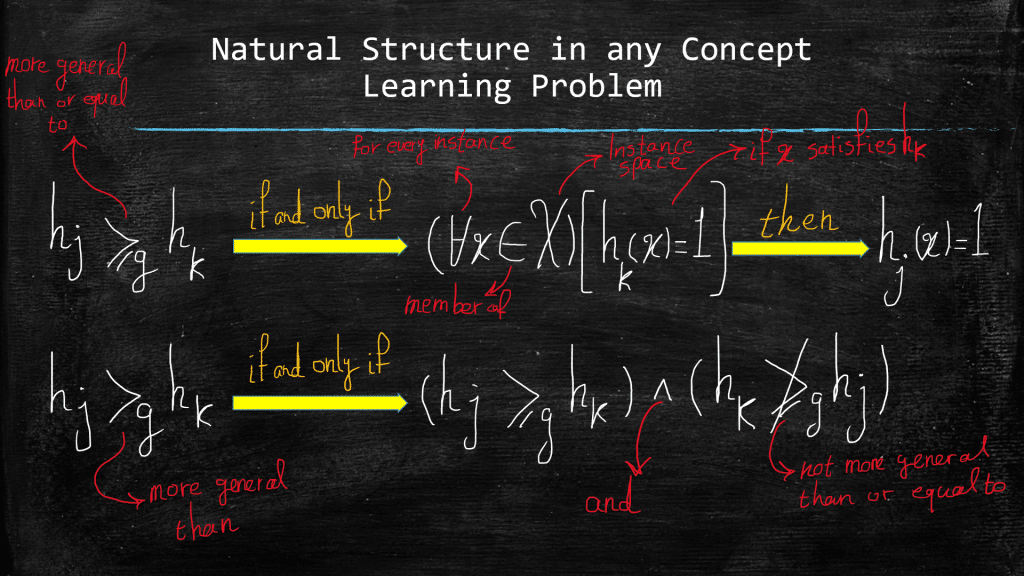
Finally, there are cases where it just makes sense to look at the same definition but from a different angle. So, after understanding what more general means, we can also consider the other side of the spectrum. Meaning that, if hypothesis h_k is more general than h_j then we can say, equivalently, that h_j is more specific than h_k. This is just another way for saying the same thing.

Let's Get More Visual, Shall We...

Let’s consider the following hypotheses from our table:

h1 = <sunny, ?, strong>

h2 = <sunny, ?, ?>

h3 = <sunny, warm, ?>

Now, based on what we learned regarding ≥_g relation, can you compare these hypotheses and determine which one is more general than or equal to the others?

If we look closely, we can see that all the instances that satisfy both h1 and h3, also satisfy h2, so we can say that:

h2 ≥_g h1 and h3

But what about the relationship between h1 and h3? Can we conclude anything regarding these 2? Yes we can, and here it is: Neither h1 nor h3 are more general than each other! Look closer and determine why this is the case!

hint: You should find instances that can satisfy h3 but not h1 to prove that h1 is NOT more general than h3. Same story but the other way around to prove that h3 is not more general than h1.

Super Important Note!!!

Remember that both ≥_g and >_g relationships are defined absolutely INDEPENDENT of the target concept! In both cases, we are interested in the instances that satisfy the hypotheses, regardless of their classification label (i.e., target concept value, ground-truth).

In the next post, we will focus on the algorithms that take advantage of both ≥_g and >_g relationships in order to make the search in the hypothesis space more efficient and basically practically feasible and smart.

Best of Luck! ML-Dawn